CVillain
[알고리즘] 버블 정렬(Bubble Sort) 본문
다음 숫자들을 오름차순으로 정렬하시오.
2, 5, 4, 1, 3
버블 정렬 또한 선택 정렬과 마찬가지로 몹시 직관적인 정렬 방법이다!
바로 옆에 있는 숫자를 비교해서 더 작은 숫자를 앞으로 보내는 방법으로 동작한다.
※ 버블 정렬은 정렬 알고리즘 중에서 구현은 가장 쉽지만 가장 비효율적인 알고리즘
그림으로 살펴보자!
먼저 첫 번째 자리를 구하는 방법이다.

바로 옆에 있는 숫자와 비교해서 더 작은 숫자를 앞으로 보냈다.
두 번째 자리 숫자를 구하는 방법도 같다.

첫 번째 자리는 구했으므로 두 번째까지만 비교를 한다.
계속해서 세 번째 자리를 구해보면 다음과 같다.
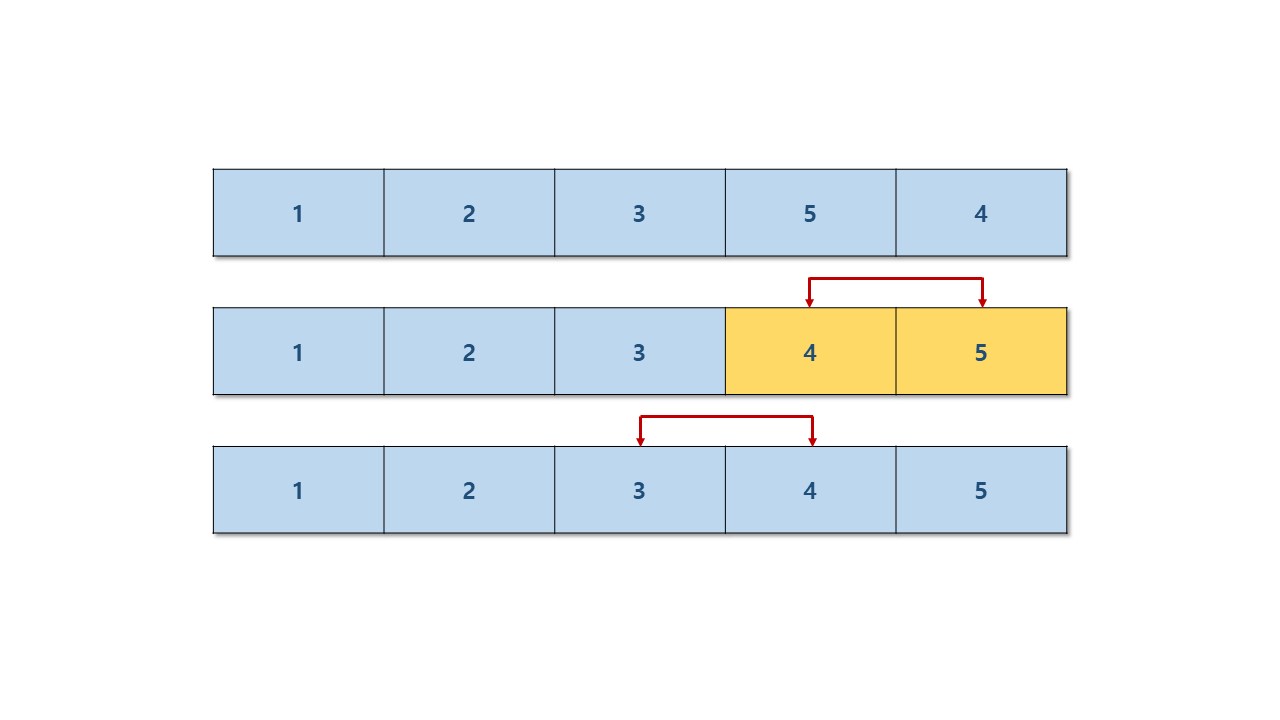
이미 정렬이 되었으므로 네 번째 자리는 바꿀 필요가 없다.
코드로 확인해보면 다음과 같다.
public class Main {
public static void main(String[] args) {
int[] arr = {2, 5, 4, 1, 3};
for(int i=0; i<5; i++) {
for(int j=4; j>i; j--) {
if(arr[j-1] > arr[j]) {
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
}
}
for(int i=0; i<5; i++) {
System.out.print(arr[i] + " ");
}
}
}
각 cycle마다 가장 작은 값이 맨 앞으로 보내지게 되는데, 반대로 가장 큰 값이 맨 뒤로 보내져도 상관없다. 이처럼 단순하게 반복해서 연산을 하게 되면 수행시간이 늘어나게 된다. 즉, 비효율적인 알고리즘이라고 할 수 있다.
시간 복잡도는 선택 정렬과 동일하다.
버블 정렬의 시간 복잡도는 O(N2)이다.
'Algorithm > Theory' 카테고리의 다른 글
| [알고리즘] 삽입 정렬(Insertion Sort) (0) | 2021.09.04 |
|---|---|
| [알고리즘] 선택 정렬(Selection Sort) (0) | 2021.09.02 |
| [알고리즘] 카탈란 수(Catalan number) (0) | 2021.08.31 |
Comments



